+ - 0:00:00
Notes for current slide
Notes for next slide

R Basics

Introduction to Data Science (BIOL7800)

https://introdatasci.dlilab.com/

Daijiang Li

LSU

2023/09/12

1 / 25

Data types

The first step in any data analysis is to choose the structure and to create a dataset to hold the data

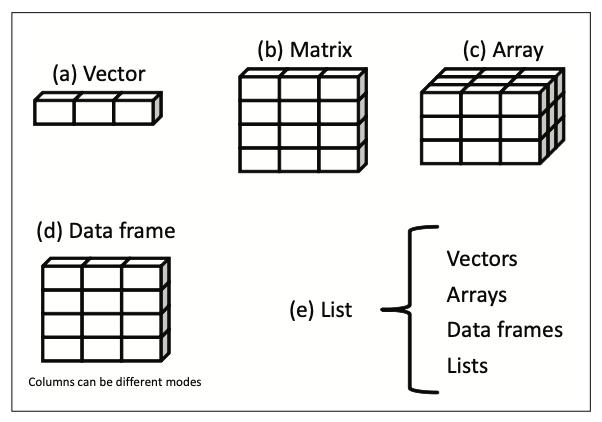
R has a wide variety of structures for holding data, including scalars, vectors, arrays, data frames, and lists.

2 / 25

Data structures

Dimensions Homogeneous Heterogeneous
1d Vector (atomic) List (generic)
2d Matrix Data frame
nd Array NA

Almost all other objects are build upon these foundations.

str() to understand data structure

data structure in R

3 / 25

Vector

Vector types: logical, double, integer1 , character, complex (imaginary numbers), and raw (bytes)

Go-to function for making vectors: c()

(a <- c(1:3)) # equal to: a <- c(1:3); a
## [1] 1 2 3
(b <- c(4:6))
## [1] 4 5 6
(C <- c(a, b)) # don't name it as c!
## [1] 1 2 3 4 5 6

[1] double and integer are both numeric

4 / 25

Vector

Vectors have three common properties:

  • Type (what it is), typeof()
  • Length (how many elements), length()
  • Attributes (additional arbitrary metadata) attributes()
typeof(a)
## [1] "integer"
length(a)
## [1] 3
attributes(a)
## NULL
5 / 25

Vector

(v_dbl = c(1, 3.1))
## [1] 1.0 3.1
(v_int = c(0L:3L)) # colon operator
## [1] 0 1 2 3
(v_log = c(TRUE, FALSE)) # T, F
## [1]  TRUE FALSE
(v_chr = c("a", "word"))
## [1] "a"    "word"
6 / 25

Vector

(v_dbl = c(1, 3.1))
## [1] 1.0 3.1
(v_int = c(0L:3L)) # colon operator
## [1] 0 1 2 3
(v_log = c(TRUE, FALSE)) # T, F
## [1]  TRUE FALSE
(v_chr = c("a", "word"))
## [1] "a"    "word"
typeof(v_dbl)
## [1] "double"
is.double(v_dbl)
## [1] TRUE
is.numeric(v_int)
## [1] TRUE
is.integer(v_int)
## [1] TRUE
is.atomic(v_log)
## [1] TRUE
6 / 25

Coercion

Vector only allow one type of elements; so when mix different types of elements, they will be coerced to the most flexible type (least to most flexible: logical, integer, double, character)

c(v_log, v_int)
## [1] 1 0 0 1 2 3
c(v_log, v_chr)
## [1] "TRUE"  "FALSE" "a"     "word"
c(v_dbl, v_int)
## [1] 1.0 3.1 0.0 1.0 2.0 3.0
c(v_dbl, v_chr)
## [1] "1"    "3.1"  "a"    "word"
typeof(c(v_log, v_int))
## [1] "integer"
typeof(c(v_log, v_chr))
## [1] "character"
typeof(c(v_dbl, v_int))
## [1] "double"
typeof(c(v_dbl, v_chr))
## [1] "character"
7 / 25

Coercion and math functions

Coercion often happens automatically

v_log2 = c(TRUE, FALSE, TRUE, TRUE, FALSE)
sum(v_log2)
## [1] 3
mean(v_log2)
## [1] 0.6
8 / 25

How do you get the number of positive values in the vector below using the coercion example in the previous slide?

v_norm = rnorm(n = 1000, mean = 0, sd = 2)
head(v_norm, n = 10)
##  [1] -1.10087437  1.28091634  1.51635608 -2.67190898  2.76741063  1.37167187
##  [7] -3.43942011 -1.20752287  0.07888408 -0.81300381
9 / 25

take a minute to discuss with others

Coercion on purpose

as.integer(v_log2)
## [1] 1 0 1 1 0
as.character(v_dbl)
## [1] "1"   "3.1"
as.logical(v_int)
## [1] FALSE  TRUE  TRUE  TRUE
as.numeric(v_log2)
## [1] 1 0 1 1 0
as.numeric(v_chr)
## Warning: NAs introduced by coercion
## [1] NA NA
10 / 25

Vector names

Three ways to add names

(v1 = c(a = 1, b = 2)) # 1
## a b 
## 1 2
v2 = 1:2
names(v2) = c("a", "b") # 2
v2
## a b 
## 1 2
setNames(1:2, c("a", "b")) # 3
## a b 
## 1 2
11 / 25

Vector names

Three ways to add names

(v1 = c(a = 1, b = 2)) # 1
## a b 
## 1 2
v2 = 1:2
names(v2) = c("a", "b") # 2
v2
## a b 
## 1 2
setNames(1:2, c("a", "b")) # 3
## a b 
## 1 2

Remove names

unname(v1)
## [1] 1 2
names(v2) = NULL
v2
## [1] 1 2
11 / 25

Lists

Lists are different from atomic vectors above because their elements can be of any type, including lists (thus they are recursive vectors)

x = list(1:3, "a", c(TRUE, FALSE), list(2:1, "b"))
str(x)
## List of 4
##  $ : int [1:3] 1 2 3
##  $ : chr "a"
##  $ : logi [1:2] TRUE FALSE
##  $ :List of 2
##   ..$ : int [1:2] 2 1
##   ..$ : chr "b"
is.recursive(x)
## [1] TRUE
12 / 25

Lists

l1 = list(list(1, 2), c(3, 4))
str(l1)
## List of 2
##  $ :List of 2
##   ..$ : num 1
##   ..$ : num 2
##  $ : num [1:2] 3 4
l2 = c(list(1, 2), c(3, 4))
str(l2)
## List of 4
##  $ : num 1
##  $ : num 2
##  $ : num 3
##  $ : num 4
13 / 25

Lists

l1 = list(list(1, 2), c(3, 4))
str(l1)
## List of 2
##  $ :List of 2
##   ..$ : num 1
##   ..$ : num 2
##  $ : num [1:2] 3 4
l2 = c(list(1, 2), c(3, 4))
str(l2)
## List of 4
##  $ : num 1
##  $ : num 2
##  $ : num 3
##  $ : num 4
typeof(l1)
## [1] "list"
unlist(l1) # back to atomic vector
## [1] 1 2 3 4
13 / 25

List names

names(l2)
## NULL
names(l2) = c("name_1", "name_2")
str(l2)
## List of 4
##  $ name_1: num 1
##  $ name_2: num 2
##  $ NA    : num 3
##  $ NA    : num 4
l3 = list(lst_a = c(1:5), lst_b = letters[1:3], LETTERS[1:3])
str(l3)
## List of 3
##  $ lst_a: int [1:5] 1 2 3 4 5
##  $ lst_b: chr [1:3] "a" "b" "c"
##  $      : chr [1:3] "A" "B" "C"
names(l3)
## [1] "lst_a" "lst_b" ""
14 / 25

Matrix

matrix(data = 0, 
       nrow = 3, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    0    0    0
## [2,]    0    0    0
## [3,]    0    0    0
matrix(data = 1:9, 
       nrow = 3, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9
15 / 25

Matrix

matrix(data = 0, 
       nrow = 3, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    0    0    0
## [2,]    0    0    0
## [3,]    0    0    0
matrix(data = 1:9, 
       nrow = 3, ncol = 3)
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9
matrix(data = letters[1:9], 
       nrow = 3, ncol = 3)
##      [,1] [,2] [,3]
## [1,] "a"  "d"  "g" 
## [2,] "b"  "e"  "h" 
## [3,] "c"  "f"  "i"
matrix(data = LETTERS[1:9], 
       nrow = 3, ncol = 3)
##      [,1] [,2] [,3]
## [1,] "A"  "D"  "G" 
## [2,] "B"  "E"  "H" 
## [3,] "C"  "F"  "I"
15 / 25

Matrix

mat_a <- matrix(data = 1:9, nrow = 3, ncol = 3,
                  byrow = TRUE 
                )
mat_a
##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9
rownames(mat_a) <- c("row1", "row2", "row3")
colnames(mat_a) <- c("col1", "col2", "col3")
mat_a
##      col1 col2 col3
## row1    1    2    3
## row2    4    5    6
## row3    7    8    9
16 / 25

Matrix

Coercion

mat_b <- mat_a
mat_b[9] = "n9"
mat_b
##      col1 col2 col3
## row1 "1"  "2"  "3" 
## row2 "4"  "5"  "6" 
## row3 "7"  "8"  "n9"
class(mat_b)
## [1] "matrix" "array"
typeof(mat_b)
## [1] "character"
17 / 25

matrix also has type conversion

Matrix

upper.tri(mat_a, diag = FALSE)
##       [,1]  [,2]  [,3]
## [1,] FALSE  TRUE  TRUE
## [2,] FALSE FALSE  TRUE
## [3,] FALSE FALSE FALSE
mat_a
##      col1 col2 col3
## row1    1    2    3
## row2    4    5    6
## row3    7    8    9
(idx = lower.tri(mat_a, 
                 diag = TRUE))
##      [,1]  [,2]  [,3]
## [1,] TRUE FALSE FALSE
## [2,] TRUE  TRUE FALSE
## [3,] TRUE  TRUE  TRUE
mat_a[idx]
## [1] 1 4 7 5 8 9
18 / 25

Arrays

a = array(data = 1:12, 
          dim = c(2, 3, 2))
a
## , , 1
## 
##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
## 
## , , 2
## 
##      [,1] [,2] [,3]
## [1,]    7    9   11
## [2,]    8   10   12
length(a)
## [1] 12
dim(a)
## [1] 2 3 2
str(a)
##  int [1:2, 1:3, 1:2] 1 2 3 4 5 6 7 8 9 10 ...
class(a)
## [1] "array"
typeof(a)
## [1] "integer"
19 / 25

Arrays: dimension names

dimnames(a) = list(c("R1", "R2"), 
                   c("C1", "C2", "C3"), 
                   c("A", "B"))
a
## , , A
## 
##    C1 C2 C3
## R1  1  3  5
## R2  2  4  6
## 
## , , B
## 
##    C1 C2 C3
## R1  7  9 11
## R2  8 10 12
20 / 25

Arrays: dimension names

dimnames(a) = list(c("R1", "R2"), 
                   c("C1", "C2", "C3"), 
                   c("A", "B"))
a
## , , A
## 
##    C1 C2 C3
## R1  1  3  5
## R2  2  4  6
## 
## , , B
## 
##    C1 C2 C3
## R1  7  9 11
## R2  8 10 12
a2 = array(data = 1:12, 
          dim = c(2, 3, 2),
          dimnames = 
            list(c("R1", "R2"), 
                   c("C1", "C2", "C3"), 
                   c("A", "B")))
a2
## , , A
## 
##    C1 C2 C3
## R1  1  3  5
## R2  2  4  6
## 
## , , B
## 
##    C1 C2 C3
## R1  7  9 11
## R2  8 10 12
20 / 25

How the three objects below are different from vector 1:5?

x1 = array(1:5, c(1, 1, 5))
x2 = array(1:5, c(1, 5, 1))
x3 = array(1:5, c(5, 1, 1))
21 / 25

Data frames

A data frame is more general than a matrix in that different columns can be different modes of data; it will be the most common data structure we'll deal with in R.

d = data.frame(v_dbl, v_log, v_chr)
d
##   v_dbl v_log v_chr
## 1   1.0  TRUE     a
## 2   3.1 FALSE  word
str(d)
## 'data.frame':    2 obs. of  3 variables:
##  $ v_dbl: num  1 3.1
##  $ v_log: logi  TRUE FALSE
##  $ v_chr: chr  "a" "word"
length(d)
## [1] 3
22 / 25

Data frames

A data frame is just a list of equal-length vectors; therefore it shares properties of both matrix and list

d
##   v_dbl v_log v_chr
## 1   1.0  TRUE     a
## 2   3.1 FALSE  word
# a list of equal length vector
typeof(d)
## [1] "list"
class(d)
## [1] "data.frame"
is.data.frame(d)
## [1] TRUE
names(d)
## [1] "v_dbl" "v_log" "v_chr"
colnames(d)
## [1] "v_dbl" "v_log" "v_chr"
rownames(d)
## [1] "1" "2"
23 / 25

as.data.frame()

as.data.frame(c(1:2))
##   c(1:2)
## 1      1
## 2      2
as.data.frame(mat_a)
##      col1 col2 col3
## row1    1    2    3
## row2    4    5    6
## row3    7    8    9
as.data.frame(l2)
##   name_1 name_2 NA. NA..1
## 1      1      2   3     4
24 / 25

Combine data frames

stack data frames

d_row = data.frame(1, 2, "3")
names(d_row) = names(d)
rbind(d, d_row)
##   v_dbl v_log v_chr
## 1   1.0     1     a
## 2   3.1     0  word
## 3   1.0     2     3
dplyr::bind_rows(d, d_row)
##   v_dbl v_log v_chr
## 1   1.0     1     a
## 2   3.1     0  word
## 3   1.0     2     3

data frames side by side

d_col = data.frame(x1 = 1:2)
cbind(d, d_col)
##   v_dbl v_log v_chr x1
## 1   1.0  TRUE     a  1
## 2   3.1 FALSE  word  2
dplyr::bind_cols(d, d_col)
##   v_dbl v_log v_chr x1
## 1   1.0  TRUE     a  1
## 2   3.1 FALSE  word  2
25 / 25

Data types

The first step in any data analysis is to choose the structure and to create a dataset to hold the data

R has a wide variety of structures for holding data, including scalars, vectors, arrays, data frames, and lists.

2 / 25
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow