Homework assignments

Homework 1

At this moment, you should have installed all required tools on your computer. You also should have some general ideas about what they can do. In this assignment, you will:

Register a GitHub account and create a new private repository named as BIOL7800.
Within the repository, add an RStudio project file; you can name it as biol7800.Rproj.
Create a folder named as homework; and then a subfolder named as hw_01.
Within hw_01, create a RMarkdown file named as hw_01.Rmd. You can use the default template for it.
Replace the content with a short self introduction of yourself. Try to use some markdown syntax (e.g., section title, bold, italic fonts, etc.).
Also insert bash chunks to print out the versions of git and R installed on your computer.

After done, compile the Rmd file to html and pdf. Push all files (Rmd, html, and pdf) to your BIOL7800 repository on GitHub. You need to add me as a collaborator for your repository. This repository is where you are going to submit all homework assignments and final reports. I will grade it by cloning it to my computer and recompile it. The last commit time will be used to check whether it is late or not. Remember, no late homework will be accepted. If the last commit time is after the deadline, I will use whatever commit that was before the deadline as your submission.

This homework will be due at September 14th, 9am.

Homework 2

(2 points) Fix each of the following common data frame subsetting errors:

mtcars[mtcars$cyl < 6]
mtcars[-1:3,]
mtcars[mtcars$cyl = 8, ]
mtcars[mtcars$cyl == 4 | 6, ]

(1 point) Why does the following code generated five missing values?
```
x = 1:5
x[NA]
```
(2 points) Why does mtcars[1:15] return an error? How does it differ from mtcars[1:15, ]?

(2 points) Explain how does the following code work.

x = matrix(c(1:3, NA, 5:7, NA, NA), nrow = 3)
x[is.na(x)] = 0

(3 points) Load the Car Road Tests dataset (in R, run data("mtcars"), ?mtcars), then add a new column named as mpg_2 for the mtcars data frame. You can use if ... else ... or ifelse or any other functions that can get the job done. This new column will categorize mpg into four categories using the thresholds below:

mpg_2 category Thresholds

Low mpg < 16

Low_intermediate 16 <= mpg < 21

Intermediate_high 21 <= mpg < 26

High 26 <= mpg

`mpg_2` category	Thresholds
Low	mpg < 16
Low_intermediate	16 <= mpg < 21
Intermediate_high	21 <= mpg < 26
High	26 <= mpg

This homework will be due at September 28th, 9am. Please submit your homework as an Rmd file to GitHub. It is probably a good idea to create a hw_02 subfolder within your homework folder and put the Rmd file there. Please also generate a PDF file there. You don’t need to email me again about your homework. I have your GitHub repo link and will check out your homework there. This should apply to all homework assignments.

Homework 3

(2 points) Suppose we have a dataset A (see code below) where each column represents multiple measures of nitrogen concentration in a particular lake. We want to get the average value for each lake. Do this in two ways: a for loop and a vectorized function colMeans().
```
set.seed(12) # to be reproducible
A = matrix(data = runif(n = 1:500), nrow = 50, ncol = 10)
colnames(A) = paste("lake", 1:10, sep = "_")
```
(2 points) From the for loop lecture, we see the following example of using apply():
```
x = array(1:27, dim = c(3, 3, 3))
apply(X = x, MARGIN = c(1, 2), 
      FUN = paste, collapse = ", ")
```
Now, use for loops to get the same task done (hint: nested loops). The results should be the same.
(2 points) The Fibonacci Sequence is the series of numbers that the next number is the sum of the previous two numbers: 0, 1, 1, 2, 3, 5, 8 … Use a for loop to get the first 30 numbers of the Fibonacci Sequence. This question should demonstrate the need for loops because there is no easy way to use vectorized functions in this case.
(2 points) In the example data below, extract those ranking numbers with regular expression. The results should have the number(s) and . if it follows after the numbers immediately (i.e., 1., 12., 105., 105.3, etc.). Remove empty strings from the final results. You should get 107 strings for your results.
```
top105 = readLines("http://www.textfiles.com/music/ktop100.txt")
top105 = top105[-c(64, 65)] # missing No. 54 and 55
```
(2 points) For the vector with length of 107 you got from question 4, remove all trailing .. (hint: ?sub). Then convert it to a numeric vector and find out which numbers have duplications (i.e., a tie in ranking). Don’t count by eyes, use R to find it out (hint: table(), sort(); or duplicated(), which(), [ subsetting; there are more than one way to do so).

This homework will be due at October 12th, 9am.

Homework 4

(3 points) Use the rvest R package to scrape the schedule and materials table into R from the course webpage (https://introdatasci.dlilab.com/schedule_materials/). Read the documentation of rvest so you get a better idea about the functions provided by rvest and their usages.
(2 points) With the extracted data frame, create two new columns based on the Date column: month and day. month would be the month abbrevations from the Date column; day would be the numeric numbers from the Date column. Although you can use whatever approach to get this done (do not enter them by hand…), I suggest you try to practice regular expression here (sub() or stringr::str_extract()).
(2 points) With the data frame generated from Q2, use group_by() and summarise() to find out the number of lectures for each month, order the results by the number of lectures (high to low).
(3 points) For the Topic column, split all values into words (hint: stringr::str_split()). Observe the values in the Topic column and use regular expression to specify the pattern in the stringr::str_split() or strsplit() function. Once this is done, you should get a list of list, you can use unlist() to convert it into a vector and name it as words. Use table() and sort() to find the top 5 most frequent words.

I was thinking to have a homework to get all plant occurrence data within Baton Rouge from GBIF. But it will require you to register an account and have account name and password when you use the rgbif package. This may have the risk of get your password leaked (you can avoid this by reading the documentation of rgbif); so I decided not to do so. If you are interested, you may want to run some example codes from the rgbif package’s documentation.

This homework will be due at October 31th, 9am.

Homework 5

In the neonDivData data package, there is a data frame named as data_plant. This data frame records plant coverage (percentage at 1 m^2^ scale indicated by the sample_area_m2 column) and plant presence information in larger plots (10 and 100 m^2^ indicated by the sample_area_m2 column). Use this data frame and functions we learned during lectures to do the steps below.

(2 points) Create a new column named as genus for data_plant from the taxon_name column. The genus name is the first word of the scientific names. For example, if a record has taxon_name of "Bunchosia glandulosa (Cav.) DC.", then the genus is "Bunchosia". You probably want to use regular expression to do so. Take a look at all the names (sort(unique(data_plant$taxon_name))) to look at possible genus names and think about how to specify the regular expression pattern. Randomly select 100 values from the genus column and print it out.
(2 points) Looking at the taxon_name values, it is clear that some scientific names probably are the same species (as different subspecies). For example, we may want to treat “Calamagrostis canadensis (Michx.) P. Beauv.” and “Calamagrostis canadensis (Michx.) P. Beauv. var. langsdorffii (Link) Inman” as the same species. Create a new column taxon_name2 for data_plant based on taxon_name. taxon_name2 should just contain the first two words of taxon_name. For example, “Calamagrostis canadensis (Michx.) P. Beauv.” and “Calamagrostis canadensis (Michx.) P. Beauv. var. langsdorffii (Link) Inman” should both be “Calamagrostis canadensis”. Randomly select 100 values from the taxon_name2 column and print it out.
(2 points) Calculate the number of species (based on taxon_name2) of each site observed based on different sizes of plot:
- based on 1 m^2^ plots; this would be all observations with sample_area_m2 == "1". This would result in a data frame named as n_1 with two columns: siteID and richness_1m2.
- based on 10 m^2^ plots; this would be all observations with sample_area_m2 %in% c("1", "10"). This would result in a data frame named as n_10 with two columns: siteID and richness_10m2.
- based on 100 m^2^ plots; this would be all observations with sample_area_m2 %in% c("1", "10", "100"). This would result in a data frame named as n_100 with two columns: siteID and richness_100m2.
then, use dplyr::left_join() to join n_1, n_10, and n_100 as one data frame n_all, which should have 47 rows and four columns: siteID, richness_1m2, richness_10m2, and richness_100m2. Note: dplyr::left_join() can only join two data frames at each time, so you may use pipe (e.g., xyz = left_join(x, y) %>% left_join(z)).
(2 points) Transform n_all to a long format data frame named as n_all_long with three columns: siteID, spatial_scale, and richness. Hint: tidyr::pivot_longer().
(2 points) Use ggplot2 and n_all_long to generate the plot below. Each line links the three values of each site (hint: aes(group = siteID)).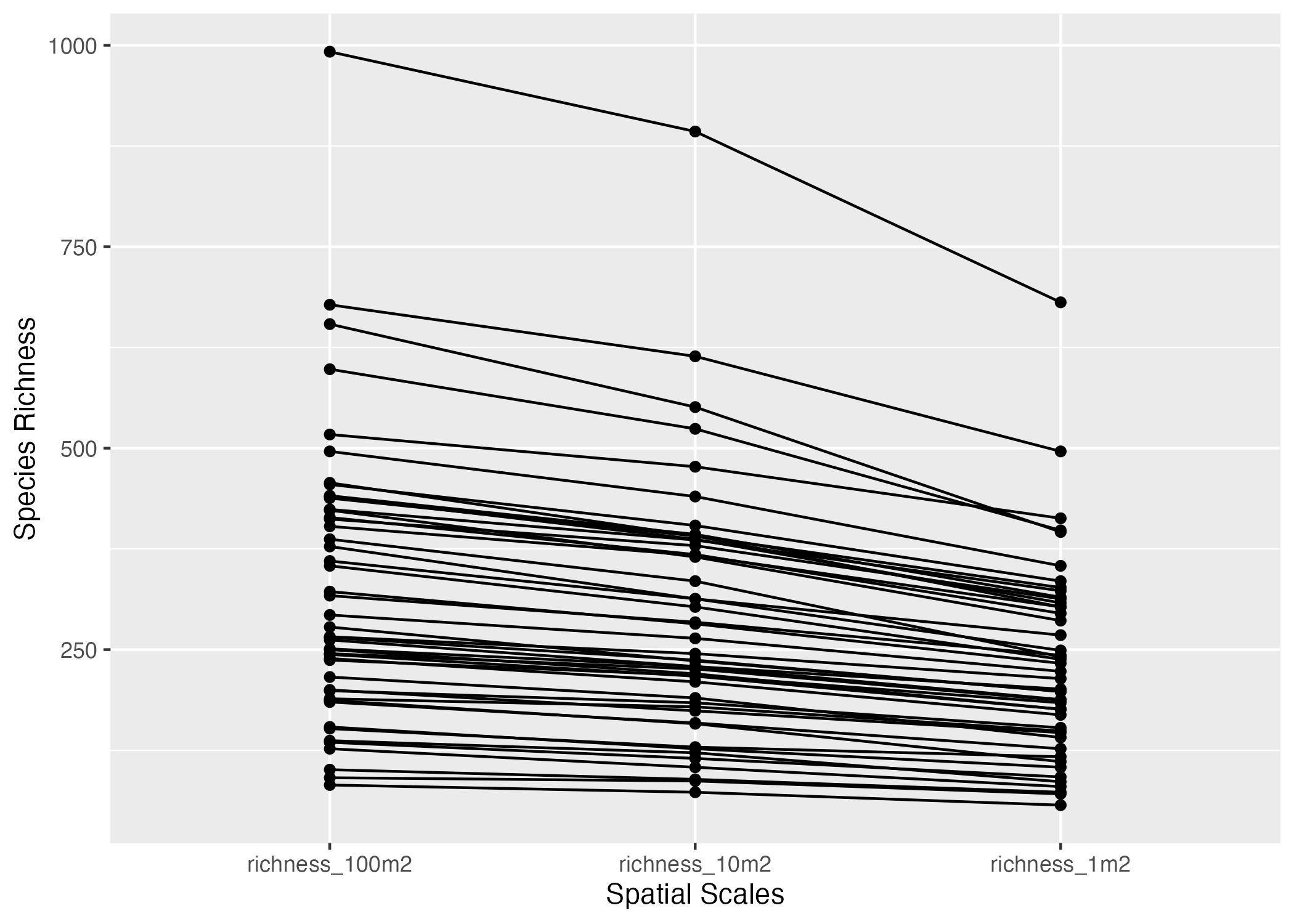

This homework will be due at November 2nd, 9am.

Homework 6

Note: Please please please write some text in your answers, do not just put R code there! Also, you should have a PDF file along with the Rmd file in your homework folder. For this homework, you can use R to get answers except 1c, where you should have a hand-calculated solution (show the process); you can use R code to verify your answer though. If you assigned anything as an object in R for your answers, remember to print it out so that I can see your results.

The data consist of a predictor variable x, plant height, and a response variable y, grain yield, for eight varieties of rice.

x = c(110.5, 105.4, 118.1, 104.5, 93.6, 84.1, 77.8, 75.6)
y = c(5.755, 5.939, 6.010, 6.545, 6.730, 6.750, 6.899, 7.862)

Consider fitting a simple linear regression model $y_i = \beta_0 + \beta_1x_i+\varepsilon_i$ where $\varepsilon_i \sim iidN(0, \sigma^2)$, i = 1, 2, …, 8.

(1 point) Give the least squares estimate ($\hat{\beta_{1}}$) of the slope $\beta_{1}$. Give a brief interpretation of $\hat{\beta_{1}}$.
(1 point) Perform a test for $H_{0}:\beta_{1}=0$ versus $H_{a}:\beta_{1}\neq0$ using an F test first and then a T test. Your conclusion?
(1 point) Construct a 95% confidence interval for the intercept $\beta_{0}$ by hand using the equation from the lecture, compare your results with those from R and briefly interpret the 95% confidence interval. You can get $t_{n-2,\alpha/2}$ using R code qt(alpha/2, n-2) where alpha is 0.05 here.
(1 point) Give the fitted regression line (as a equation that looks like $\hat{y}=a+bx$) and the raw residuals.
(1 point) Give an estimate ($\hat{\sigma}^{2}$) of the error variance ($\sigma^{2}$).
(1 point) Estimate the expected yield of a rice variety ($\mu_{0}$) that has height $x_{0}=100$ and provide a 95% confidence interval.
(1 point) Predict the yield of a new rice variety that has height $x_{0}=100$ and provide a 95% prediction interval. Compare the results with those from (f), which one is wider?
(1 point) Compute the coefficient of determination $R^{2}$ and briefly interpret what does it mean.

This problem is designed to demonstrate why residuals are plotted against $\hat{y}$ (instead of $y$). Consider the following (artificial) data set that was constructed so that the relationship between $y$ and $x$ is quadratic. It is immediately evident that a linear fit is not appropriate. However, we adopt the point of view that the residual plot will provide diagnostic information on the lack of fit.
```
x = c(1, 2, 3, 4, 5, 6, 7, 8, 9)
y = c(-2.08, -0.72, 0.28, 0.92, 1.20, 1.12, 0.68, -0.12, -1.28)
```

(0.25 point) Plot $y$ vs. $x$.
(0.25 point) Plot the raw residuals vs. $y$.
(0.25 point) Plot the raw residuals vs. $x$.
(0.25 point) Plot the raw residuals vs. $\hat{y}$.
(1 point) Compare the plots from (b), (c), and (d). Is there a meaningful difference between (c) and (d)? Explain. Which of the plots (b) or (d) gives a better indication of the lack of fit? Explain.

Note: If you were to compute the correlation between $\hat{y}$ and the raw residuals, you would find this to be 0. If you compute the correlation between the observed $y$ and the raw residuals, you find that this is $\sqrt{1-R^{2}}$ where $R^{2}=SSR/SST$. It is the absence of correlation in plot (d) — and also plot (c) — that is important. No computations of correlation are required in this problem, but you may give it a try in R.

This homework will be due at November 16th, 9am.

Homework 7

(2 points) Reorganize your BIOL7800 Github Repository to have the following structure. If your respository already has this structure, great!! You will get all the points for this question.
```
.
├── final_project
└── homework
    ├── hw_01
    ├── hw_02
    ├── hw_03
    ├── hw_04
    ├── hw_05
    ├── hw_06
    └── hw_07
```
(8 points) Create an R package and push it to your Github account. You can name it whatever you want. In the package, put two functions that you have written or you want to write. If you don’t have such functions or ideas, try this: one function to remove rows with all 0s in the matrix generated below; and the other function to remove columns with all 0s. Name the first one as rm_0s_by_row() and the other as rm_0s_by_col().
```
set.seed(123)
x = matrix(rpois(100, 0.1), 10, 10)
```
Document them! I should be able to install your package using remotes::install_github("your_github_name/pkg_name") and run your code and read documentations.

You can work out the package locally first. Once success (pass devtools::check(); no error, no warning, no note), go to Github, create a new repository, don’t add anything there yet (i.e., no README or license file added by Github). Then follow the command it provides and link your local directory to the Github repository; then commit and push it to Github repository.

Put the link to your R package Github repository in the hw_07.md file that will be found in your BIOL7800/homework/hw_07 folder (so that I know where it is).

This homework will be due at November 30th, 9am.